SIFA - Statistical Ineffective Fault Attacks

---31 Jul 2023---

This post presents the main idea of the Statistical Ineffective Fault Attack (SIFA) in [Dobraunig et al., CHES 2018]. SIFA is applicable in a very broad range of cipher implementations, even in the presence of countermeasures.

1. Background

The SIFA’s core idea is to combine the Statistical Fault Attack (SFA) and the Ineffective Fault Attack (IFA). We first recall the principles of these two attacks on AES.

SFA [Fuhr et al., FDTC 2013]

The attack is summarized to 3 phases as below:

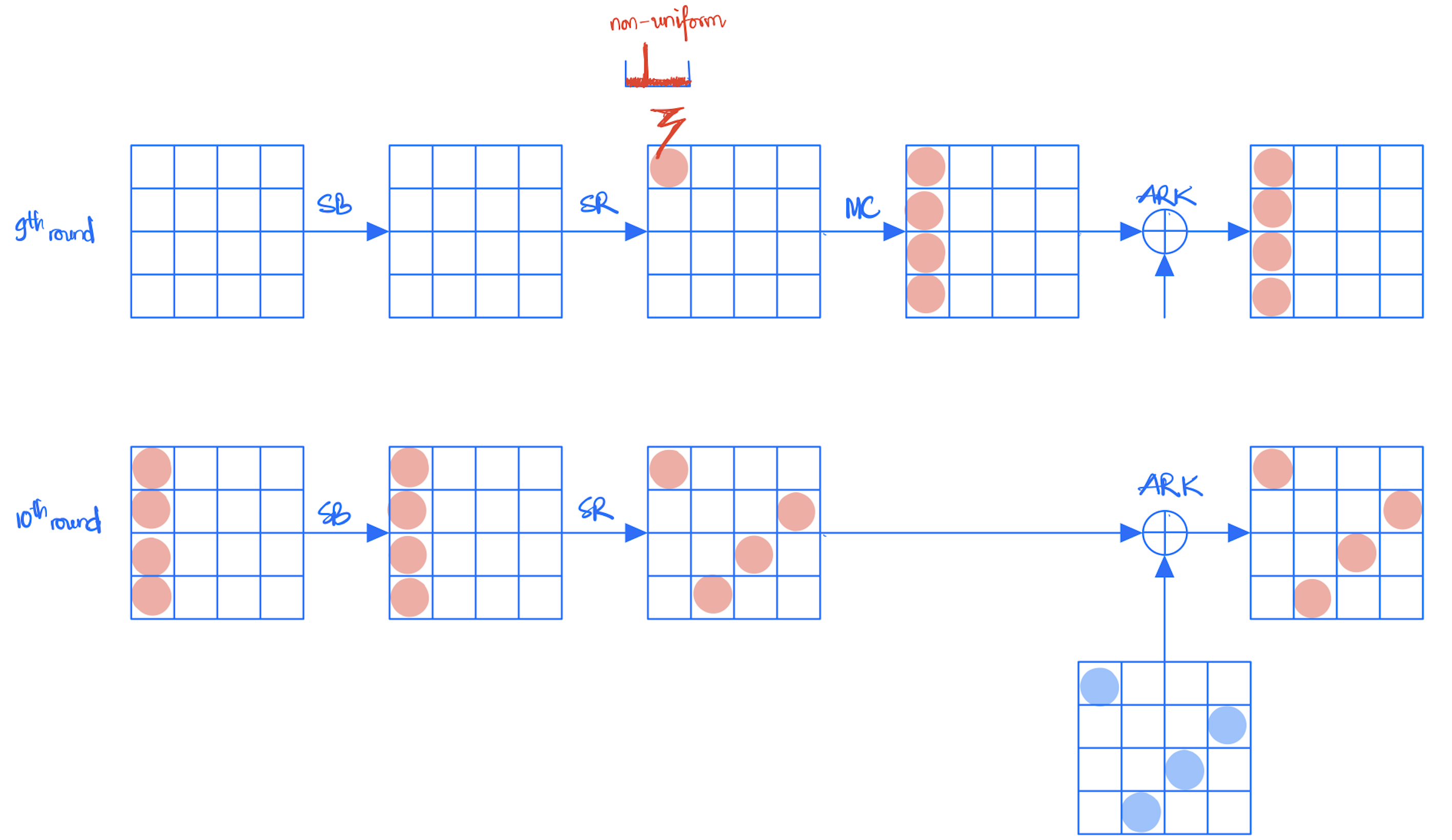
• Target one byte of the state right before the last MixColumns. Inject a fault (eg, stuck-at-0) to this byte for each encryption. This leads to a non-uniform distribution of this byte.
• Collect the faulty ciphertexts
• Use Squared Eulidean Imbalance (SEI) to exploit the non-uniform distribution of the above faulted byte by computing backwards from the ciphertexts and 4-byte hypothesis of the last round key.

IFA [Clavier, CHES 2007]

The attack is summarized to 2 phases as below:

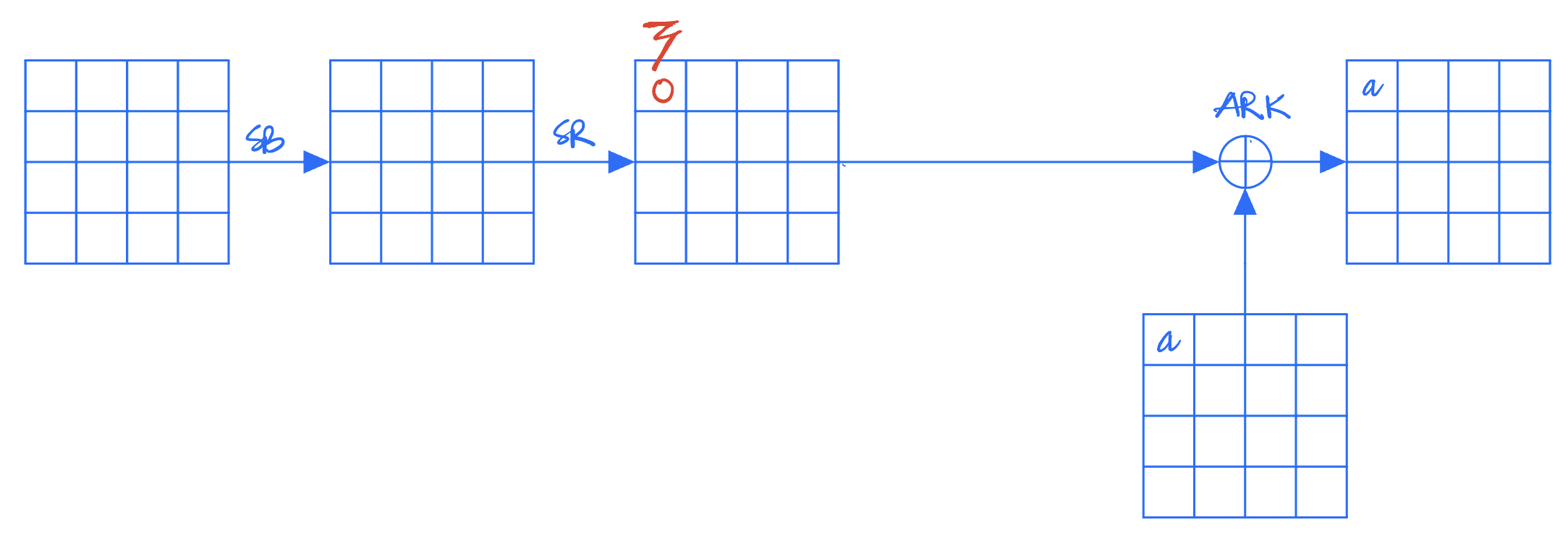
• A stuck-at-0 fault is induced in one byte of the state right before the last AddRoundKey.
• If the output is still a correct ciphertext, the fault does have any effect (ineffective fault). In other words, the targeted byte holds the value 0 and the key byte equals to the corresponding ciphertext byte.

2. SIFA

Effects of Faults

Faulting on \(x\) causes a transition from \(x\) to \(x'\). The table below (taken from the original paper) shows the fault distributions for different fault models on a 2-bit value. For instance, injecting a random-AND fault on \(x=01\) results \(x'=01\) with probability \(1/2\). This is because \(x' = x \oplus e\) where \(e \in \{00, 01, 10, 11\}\) denotes the fault. It is clear that there are 2 (out of 4) values of \(e\) which result \(x'=01\). Thus, the probability of obtaining \(x'=01\) given \(x=01\) is 1/2.

We consider the diagonals (red values) in the tables and come up with some observations:

• \(x = x'\): ineffective faults. This is IFA.
• There exists a non-uniform distribution in the probability of different transitions in the table (a) and table (b). We can exploit this non-uniform distribution to recover the key. This is SFA.

Principle

The attack is summarized to 3 phases as below:

• Target one byte of the state right before the last MixColumns. Inject a fault for each encryption. Collect the ciphertexts where the fault is not effective.
• Use Squared Eulidean Imbalance (SEI) to exploit the non-uniform distribution of the above faulted byte by computing backwards from the ciphertexts and 4-byte hypothesis of the last round key.

Discussion

We observe that the fault injection plays the role as a filter for the collected ciphertexts. For instance, using stuck-at-0 fault model to choose the ciphertexts corresponding to the value 0 at the targeted byte of the state right before the last MixColumns.

Why do we target one byte of the state right before the last MixColumns? Because the ciphertext bytes still have uniform distribution thanks to the diffusion of the last MixColumns. Then, we can make hypothesis for 4 bytes of the last round key to do the key recovery. Of course, we can target another byte in a middle round, e.g., 8th, 7th, etc. However, in that case, the backward computation from the ciphertexts is more complicated and requires more bytes for the hypothesis key.

SIFA is a robust attack. In the paper, the authors show that it can be applied in the implementations with the presence of countermeasures such as detection-based countermeasure, inefective countermeasure, infection, fault space transformation, majority voting, masking.